Area of Kite Calculator / Wind games

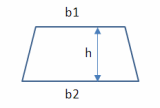
Area formula

The area of a trapezoid is given by the formula where
b1, b2 are the lengths of each base
h is the altitude (height)

Recall that the bases are the two parallel sides of the trapezoid. The altitude (or height) of a trapezoid is the perpendicular distance between the two bases.

In the applet above, click on "freeze dimensions". As you drag any vertex, you will see that the trapezoid redraws itself keeping the height and bases constant. Notice how the area does not change in the displayed formula. The area depends only on the height and base lengths, so as you can see, there are many trapezoids with a given set of dimensions which all have the same area.

Derivation of the formula

See How to derive the trapezoid area formula.

Calculator

Use the calculator on the right to calculate height, base lengths and area of a trapezoid.

Enter any three values and the missing one will be calculated. For example: enter the height and two base lengths, and press 'Calculate'. The area will be calculated.

Similarly, if you enter the area and two base lengths, the height needed to get that area will be calculated.

Finding the height given the area

How to find the height (altitude) of a trapezoid give the two bases and the area. The main area formula above has four variables (area, two bases and height). If we know any three we can always find the fourth. So for example, if we know the area and two bases we can find the height, simply by re-arranging the main formula: Where a is the area and b1, b2 are the two bases.

Finding a base from the area

How to find a base of a trapezoid give the one of the bases, the height, and the area. The main area formula above has four variables (area, two bases and height). If we know any three we can always find the fourth. So for example, if we know the area and one base and the height, we can find the missing base, simply by re-arranging the main formula: Where a is the area and is the known base, and h is the height (altitude).

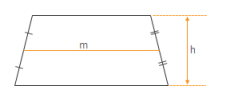
If you know the median

Recall that the median (m) of a trapezoid is the line segment linking the midpoints of the non-parallel sides. Recall also that the median's length is the average of the two parallel sides. See Median of a Trapezoid

Where is the median and h is the height (altitude).

Area as a compound shape

Another way to find the area of a trapezoid is to treat it as some simpler shapes, and then add or subtract their areas to find the result. For example, a trapezoid could be considered to be a smaller rectangle plus two right triangles: For more on this general technique, see Area of Irregular Polygons.

Coordinate Geometry

In coordinate geometry, if you know the coordinates of the four vertices, you can calculate various properties of it, including the area and perimeter. For more on this, see Trapezoid area and perimeter (Coordinate Geometry)